Time Complexity: Big O Notation Fastest to Slowest Time Complexity

Before getting into Big O Notation fastest to slowest time complexity, it’s always better to have an idea about what is Asymptotic analysis and its fundamentals. It will be really beneficial when analysing asymptotic notation in data structure with example and it will sharpen your big o coding knowledge for big o notation practice problems.
Significance of Asymptotic Notation in data structures and algorithms
Asymptotic analysis based on calculating the running time of an operation on a mathematical basis. Basically in an algorithm, the mathematical relation of run time performance can be identified by asymptotic analysis.
Why do we use asymptotic notation?
By using the asymptotic notation in design and analysis of algorithms, the time required by an algorithm to execute can be calculated and it falls under 5 categories.
5 Asymptotic Notation Analysis Types
- O − Big Oh
- Ω − Big omega
- θ − Big theta
- o − Little Oh
- ω − Little omega
Asymptotic notation and its main 3 Time complexity Analysis methods
- Lower bound ( Omega Notation ) – Minimum time required for a programme to execute.
- Tight bound ( Theta Notation ) – Average time required for a programme to execute.
- Upper bound ( Big O notation ) – Maximum time required for a programme to execute.
What are the factors that affect the running time of an algorithm?
- Speed of the computer
- The efficiency of the programming language
- Compiler performance
- Number of lines and loops in the code
- Number of operations within a loop
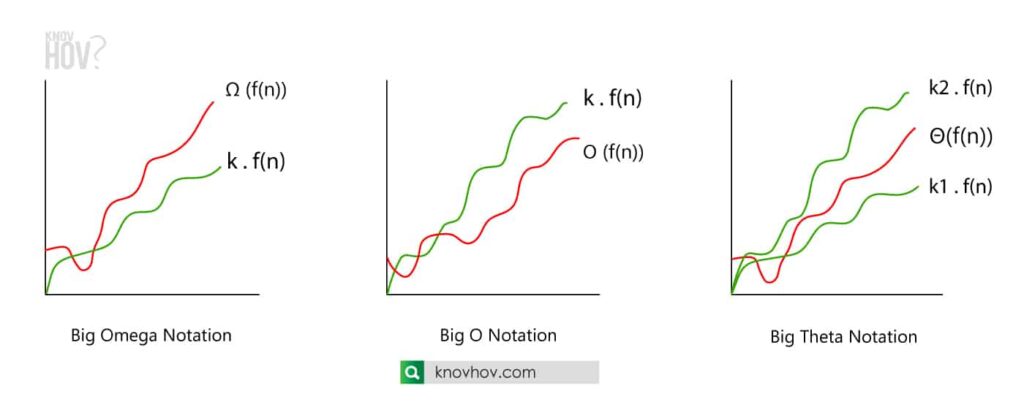
What is Big Omega notation?
Big omega notation expresses the algorithm takes at least a certain amount of time to implement. Big omega is the asymptotic lower bound of an algorithm.
For Ω (f(n)), the running time will be at least k . f(n) for a constant k.
What is Big O notation?
Big O notation explained the maximum time that the algorithm will take to implement. Analyzing an algorithm with big o notation is useful for predicting most level that the running time can be extended to. Big O notation is the asymptotic upper bound of an algorithm. It’s essential to find Big O of a function before getting an idea about its time complexity.
For O (f(n)), the running time will be at most k . f(n) for a constant k.
Modern computer science-based applications are highly using big o notation.Computer science industry applications mainly using the Big O notation to analyse algorithms and how they affect computational complexity.Big o Notation is using in order to calculate time and space requirements with respect to the increase of the input size of the algorithm.
What is Big Theta notation?
Big theta notation expresses the average exact running time performance which lies in between the upper bound and the lower bound of an algorithm. Big theta notation is the asymptotically tight bound of an algorithm.
For Θ(f(n)), the running time lies in between the least value k1 . f(n) and the most value k2 . f(n) for some constants k1 and k2.
Big O Notation fastest to slowest time complexity
The formal definition of Big O: Big O algorithm mainly gives an idea of how complex an operation is. It expresses how long time an operation will run concerning the increase of the data set which clearly describes the asymptotic time complexity.
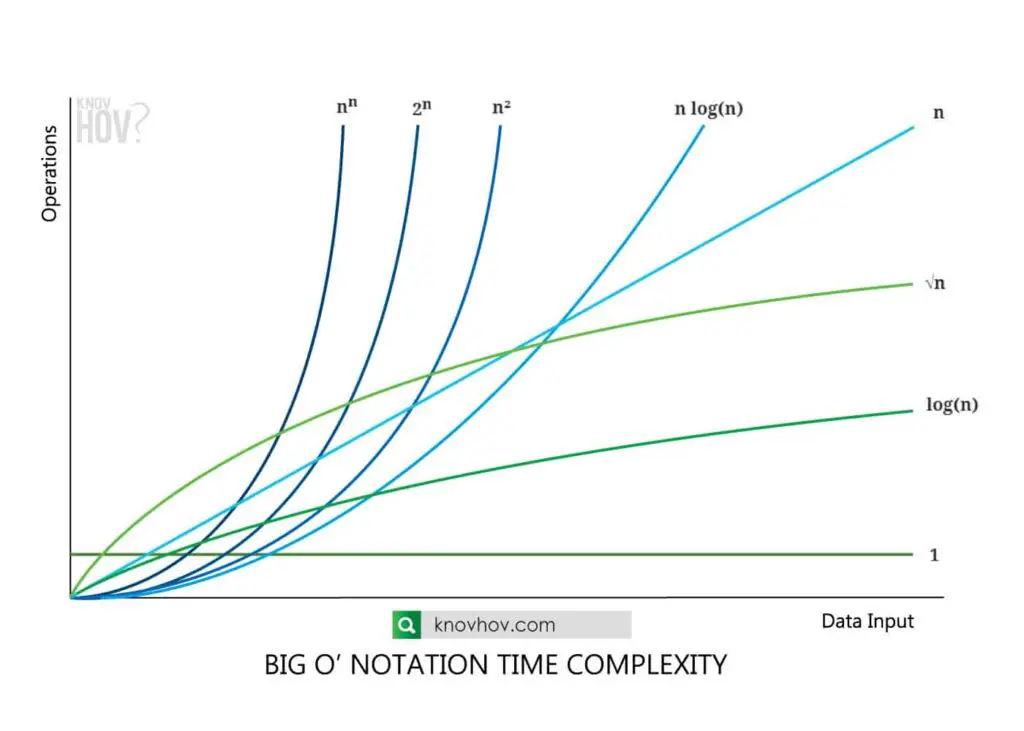
1 < log(n) < √n < n < n log(n) < n² < n³ < 2n < 3n < nn
A clarification of Big O Notation fastest to slowest ( best to worst complexity ) according to increasing order of asymptotic complexity can be implemented.
Big O Complexity Chart
| Big O function | Increasing behavior of time complexity |
| O(1) | constant |
| O(log n) | logarithmically change |
| O(n) | linear change |
| O(n log n) | Linearithmic change |
| O(n²) | Quadratic change |
| O(n³) | Cubic change |
| O(2n) | exponential change |
| O(n!) | Factorial change |
- O(1) – speed is constant. It doesn’t change with the size of the data set.
- O(log n) – Big O log n operation changes logarithmically. Little more time consuming than O(1)
- O(n) – linear change. Time taken is directly proportional to the size of the data set.
- O(n log n) – Linearithmic change in n log n big o operation. Time increases by a multiplier of 1 with the size of the data set doubles.
- O(n²) – Big O quadratic change can be seen. Time consumes four times more when the size of the data set doubles.
- O(n³) – Cubic change. Time consumes eight times more when the size of the data set doubles
- O(2n) – exponential change. time takes twice long for every new element added to the data set.
- O(n!) – Factorial change. n! Times longer time consuming directly proportional to the size of the data set.
- O(nn ) – Highest time-consuming function and the slowest to implement because of its time complexity.
This is valid for larger data sets. However n! can place anywhere between 1 < n! < nn with the change of the value of n.
Big O notation fastest to slowest time complexity can be analyzed clearly by the big o notation diagram below
What is Little oh Notation?
Big Οh notation is used to describe the tight upper-bound on the growth of an algorithm but there can also be a loose upper-bound. So the Little oh notation is used to describe an upper-bound that cannot be tight.
What is Little omega Notation?
Little omega Notation is mainly written as ω, is a notation to describe the lower bound (which is not asymptotically tight) of the growth rate on the runtime of an algorithm.
What is the importance of Big O notation in programming?
Working with large data sets is very difficult and there are many things to concern about before selecting a data structure and an algorithm to use. Analysis of Big O notation fastest to slowest time complexity gives an idea about the time taken to perform a certain algorithm and also the space complexity which expresses the amount of space that will be required by an algorithm.
Big O vs Little O: the difference between big O notation and little o notation in asymptotic notations
Little-o is a stronger condition than a big-O. Big O can be explained as the inclusive upper bound, while little o can be explained as the strict upper bound.
9 Basic things you must know before a big o coding interview
- Should be able to define the importance of asymptotic notation in algorithm analysis
- Explain various asymptotic notations with example: Best case, average case and the worst case of an algorithm
- Factors that affect the running time of an algorithm
- Define big omega notation
- Define Big O notation understanding big o notation
- Define Theta notation
- Big O Notation fastest to slowest time complexity chart
- Difference between big O notation and little o notation in asymptotic notations
- What is Little omega Notation?
FAQ:
Which time complexity is fastest?
Fastest = O(1) – Fastest time complexity because speed is constant and It doesn’t change with the size of the data set.
Which Big O notation is fastest and which is slowest?
Fastest = O(1) – The speed remains constant. It is unaffected by the size of the data set.
Slowest = O(nn ) – Because of its time complexity, the most time-consuming function and the slowest to implement.
How do you compare time complexity?
The Big O algorithm primarily indicates the complexity of an operation. It expresses how long an operation will take to run as the data set grows, which clearly describes the asymptotic time complexity.
1 < log(n) < √n < n < n log(n) < n² < n³ < 2n < 3n < nn
