How to create Transfer Functions in Matlab

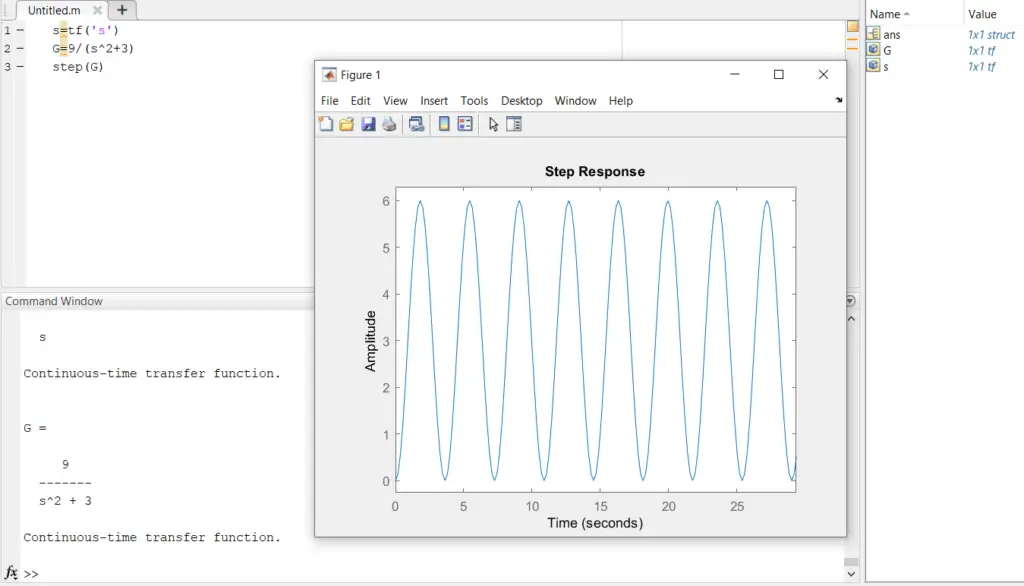
In order to create transfer functions in Matlab, Open the MATLAB command window, type the command to assign the numerator and denominator coefficient vectors of the transfer function you need to obtain.

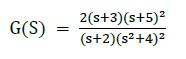
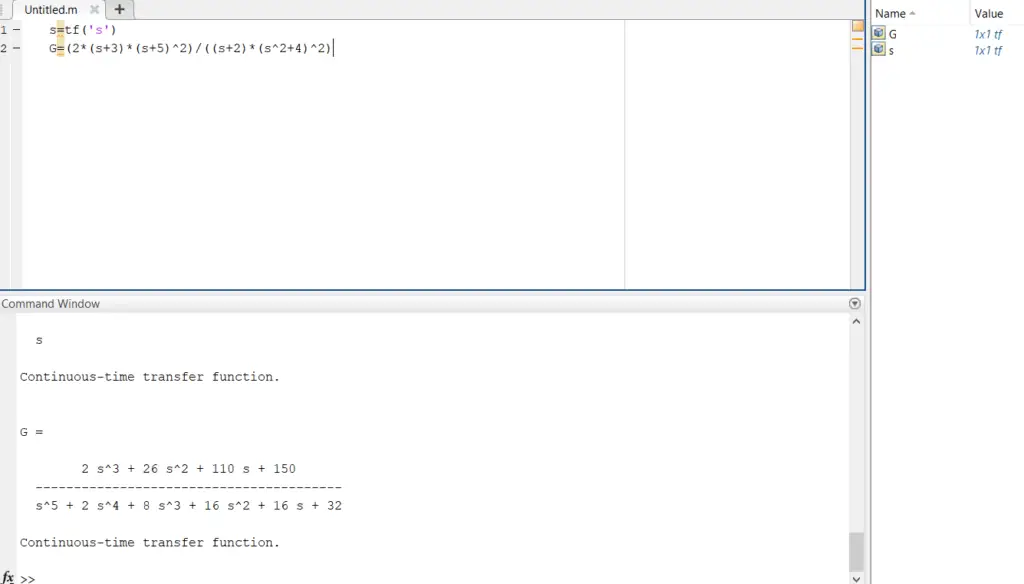
How to Find the Stability of a System in Matlab

The representation of transfer functions in Matlab is mostly helpful once analyzing system stability. By analyzing the poles (values of s where the denominator becomes zero) we can determine the stability of the system.

If all poles have negative real values, then the system can be defined as stable.

If any pole contains a positive real part, then the system is unstable.

If we tend to analyze the poles on the advanced s-plane, then all poles should be within the left half-plane (LHP) to make sure stability.

If any pair of poles are on the imaginary axis, then the system is marginally stable and also the system can oscillate.

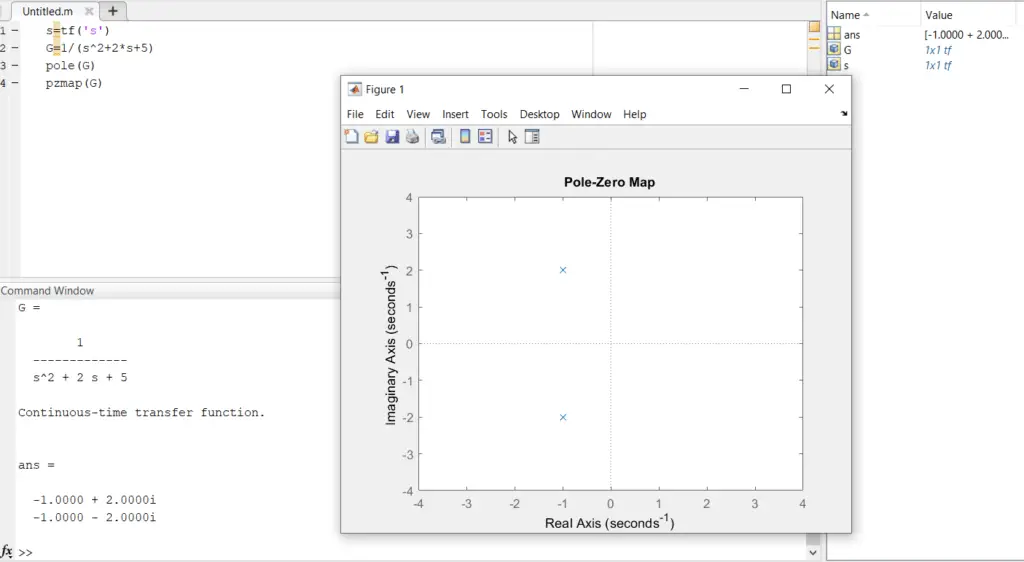
Finding the poles of the Linear Time-Invariant system model in MATLAB using “pole command”

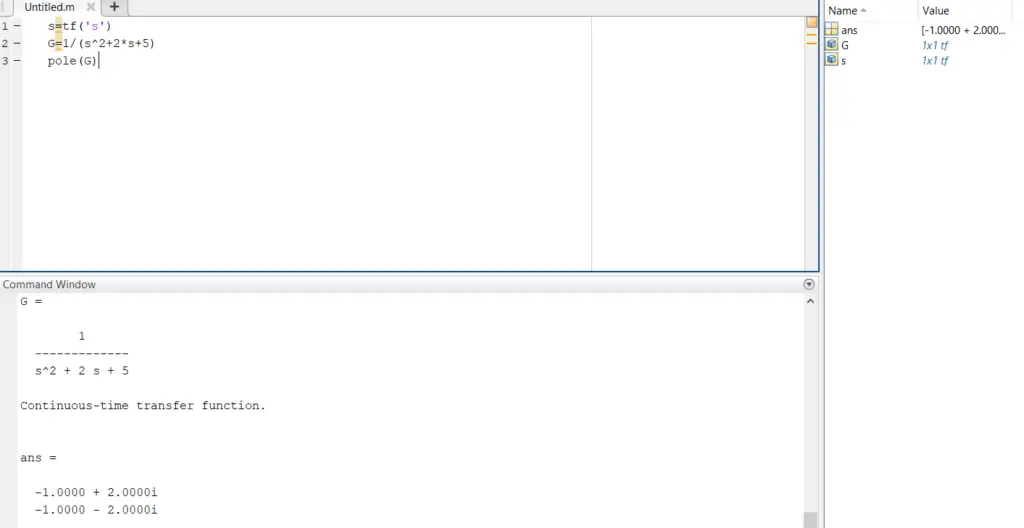
Generating the pole-zero map on MATLAB to determine the system stability

Time response of a system

Step and Impulse Responses of First Order and Second Order systems

The time response represents however the state of a dynamic system changes in time once subjected to a specific input. The time response of a linear dynamic system consists of the sum of the transient response that depends on the initial conditions and also the steady-state response that depends on the system input.

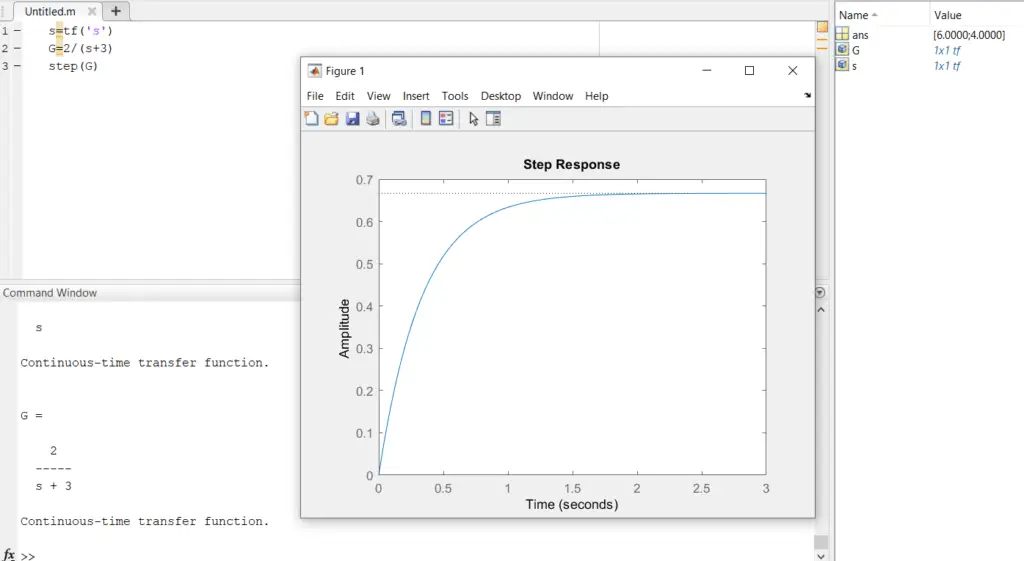
Obtaining the step response of a first-order system using MATLAB

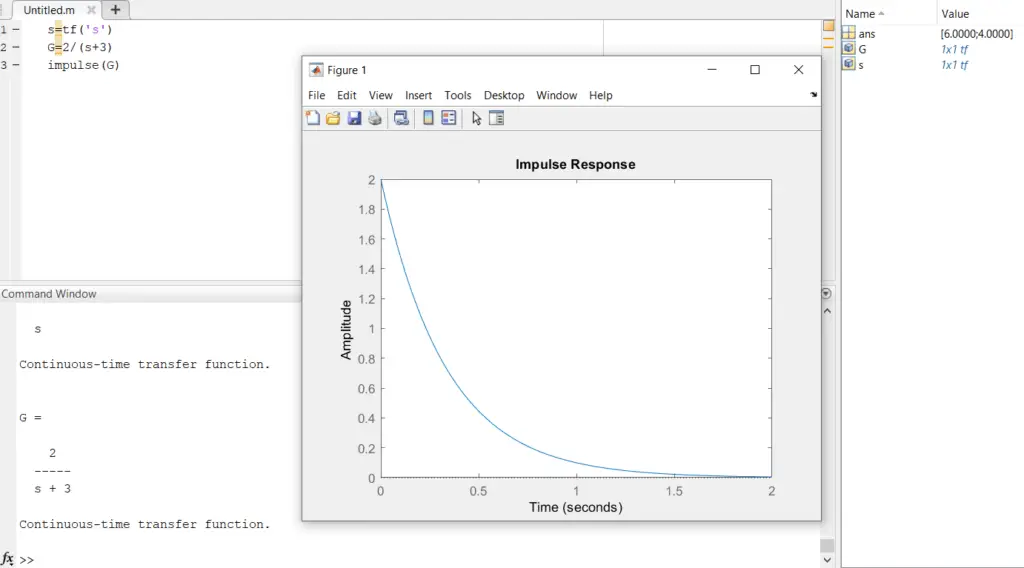
Obtaining the impulse response of a first order system using MATLAB

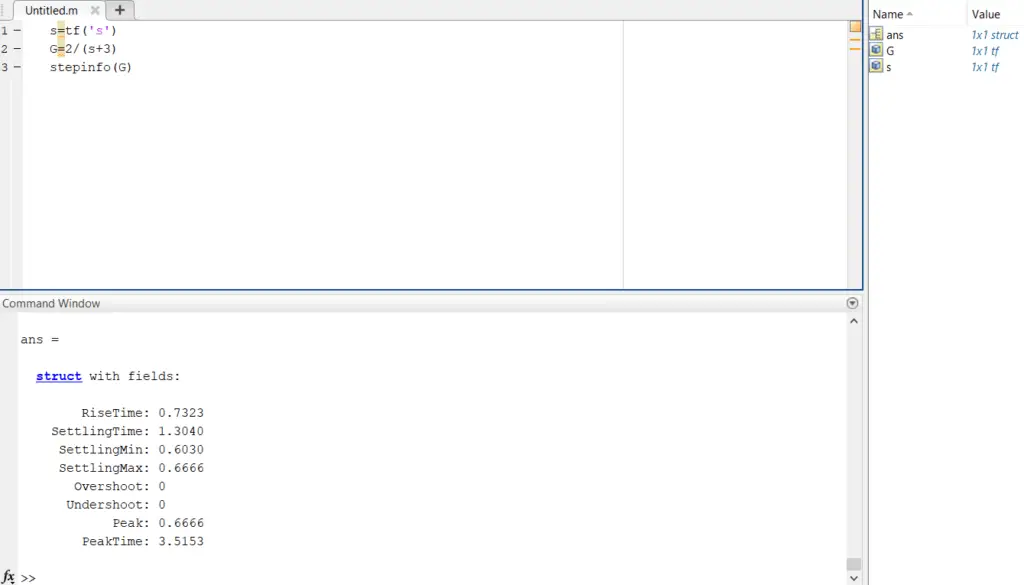
Determining the step response characteristics using MATLAB

Step time response of second order systems & their dynamic behaviour

If the input is step function then the output or the response is the step time response. The system will be described by a transfer function that has poles. Based on these poles the step response divided into four cases.

Underdamped response

During this case, the response has an overshooting with a little oscillation which ends from complex poles within the transfer function of the system

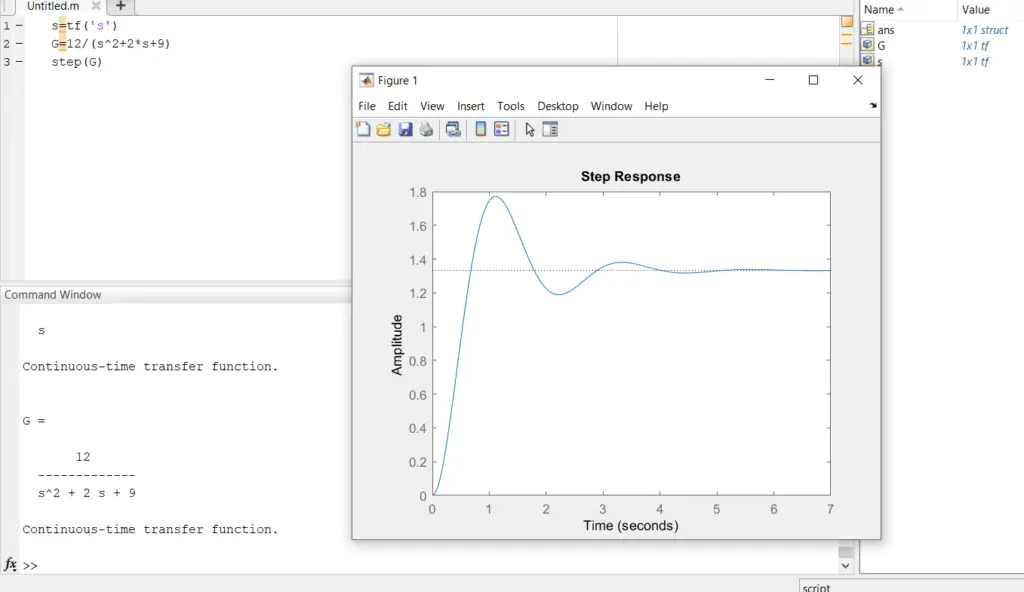
Critically damped response

During this case, the response has no overshooting and reaches the steady-state value within the quickest time. The critically damped response is the quickest response with no overshooting.

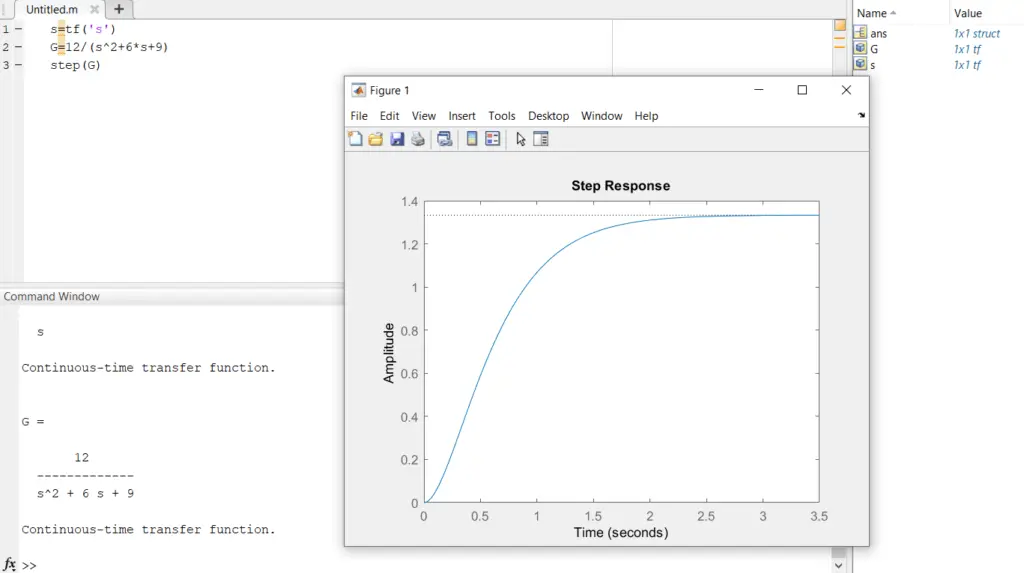
Over-damped response

During this case, no overshooting can be seen and reach the final in some in some time larger than critically case. Over damped response is results from the existence of real & distinct poles.

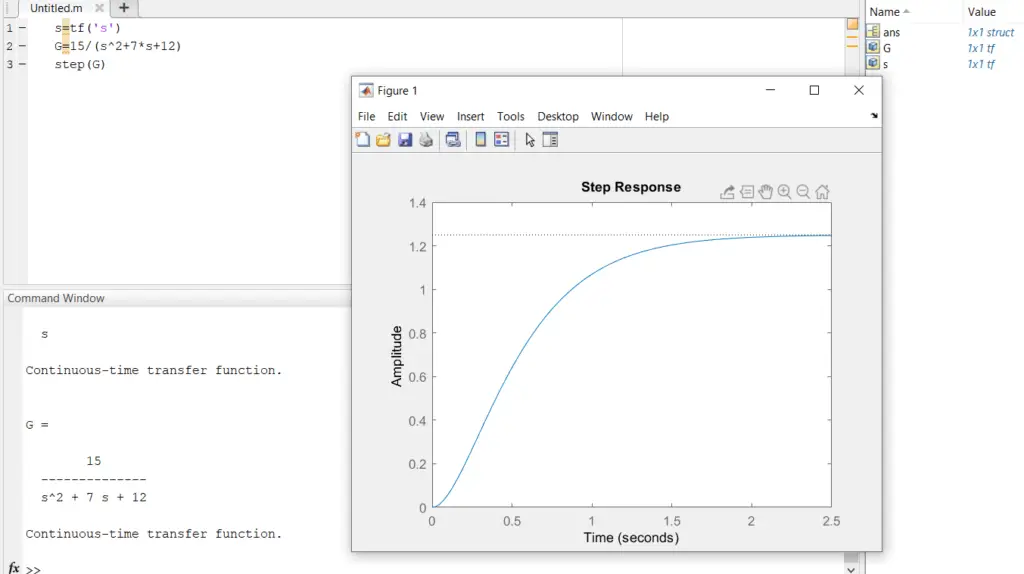
Un-damped response

During this case, a large oscillation can be seen at the output and can not reach a final value and this due to the existence of imaginary poles within the transfer function of the system and also the system during this case is named “Marginally stable”